Spielziel

James Hilton schrieb in seinem 1933 erschienenen Roman „Verlorener Horizont“ von einem versteckten Paradies, hoch in den Bergen der tibetanischen Provinz Zhongdian. In „Die Brücken von Shangrila“ erhalten Weise und Gelehrte aus dem Tiefland mit ihren Schülern in den verlassenen Dörfern des von Mythen umrankten Hochlandes Einzug, um mit ihrer Wanderschaft eine neue, vorherrschende Kultur in den Gipfeln Tibets zu errichten.

Ablauf

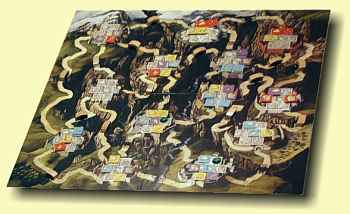
13 Dörfer ranken sich um die Gipfel der Bergriesen, stets über Bogenbrücken mit den drei bis vier nahegelegensten Dörfern verbunden. In jedem Dorf kann je ein Meister jedes Typs (Heiler, Regenmacher u.a., jeder Spieler besitzt 6 Plättchen je Symbol) Einzug erhalten. Zu Spielbeginn setzt jeder Spieler pro Typ einen Meister auf ein freies Feld in einem beliebigen Bergdorf. In der Folge ist pro Spielzug stets eine der folgenden Optionen auszuführen:

1. Ein Meisterplättchen platzieren (auf freie Felder)

2. Zwei Schüler rekrutieren (identisches Plättchen auf ein bereits gelegtes Meisterplättchen legen)

3. Eine Wanderung der Schüler veranlassen

Tragen die Optionen eins und zwei dazu bei, möglichst geschickt zusätzliche Plättchen ins Spiel zu bringen, macht Option drei den eigentlichen Reiz des Spiels aus. Ein Spieler kann, sobald auch nur ein eigener Schüler „huckepack“ in einem Dorf vorhanden ist, eine Schülerwanderung aus diesem Dorf hinaus auslösen. Dabei ziehen alle (auch die fremden) Schüler über eine der Verbindungsbrücken in ein Nachbardorf, in der Hoffnung, sich dort als neue Meister niederlassen zu können - die alten Meister bleiben im Dorf zurück. Doch nicht immer sind die Symbolfelder, die der betreffende Schüler gerne besetzen würde, im Zuwanderungsdorf frei. Während der Schüler ein freies Feld ungestört als neuer Meister einnehmen kann, kann er den Meister eines besetzten Feldes (samt Schüler) nur vertreiben, wenn das Dorf, aus dem er ausgewandert war, stärker als das Einwanderungsdorf war. Stärker heißt hierbei: Es befanden sich vor der Wanderung mehr Plättchen (Meister+Schüler) im Auswanderungsdorf. War das Auswanderungsdorf hingegen schwächer, müssen all jene wandernden Schüler, die kein freies Symbolfeld erhaschen konnten, vom Spielplan entfernt werden.

Jede Wanderung kann dabei nur einmal stattfinden, denn die Brücke, über die die Schüler zogen, zerfällt nach deren Reise wie von Geisterhand zu Staub. Wird ein Dorf dadurch schlussendlich völlig isoliert, zeigt ein daraufgelegter Stein der Weisen an, dass dieses Dorf seinen Ruhezustand erreicht hat. Sind bis auf eine alle Brücken zu Staub zerfallen, endet das Spiel. Sieger ist, wer mehr Meisterfelder in den dreizehn Dörfern für sich beanspruchen konnte.

Fazit

Die wunderschöne Optik (sieht man vielleicht von den aus Gründen der Übersichtlichkeit zwangsläufig eher schlicht gehaltenen Symbolplättchen ab) mit dem reich illustrierten Spielplan und den hölzernen Bogenbrücken mag auf den ersten Blick darüber hinwegtäuschen, dass es sich bei den Brücken von Shangrila um ein hochtaktisches Spielvergnügen handelt, das einen überaus einfachen Einstieg, aber keinerlei Glücksfaktor beinhaltet. Es gehört zur Charakteristik solcher Spiele, dass sie von manchen Spielern als „trocken“ empfunden werden. Doch den Brücken von Shangrila gelingt der Spagat zwischen knallharter Grübelei und erfrischender Kurzweiligkeit überaus gut. Zwar kommt das Spiel etwas langsam in Gang, da erst mit Einzug von genug Meistern und Schülern die raffiniert zu planenden Wanderungsbewegungen einsetzen, doch dann offenbart das Spiel ein weites Spektrum von taktischen Winkelzügen und listigen Ärgereien, das man den kurzen und einfachen Regelmechanismen spontan gar nicht zugetraut hätte. Meist benötigt man eine oder zwei Partien um zu verstehen, dass gerade die zunächst wenig beachteten Wanderungen von schwächeren in stärkere Dörfer das größte, und auch arglistigste taktische Potential beinhalten. Nicht selten bauen ein oder zwei Spieler eine Gruppe von Schülern in einem plättchenreichen Dorf auf, um damit invasionsartig ein Nebendorf auf breiter Front in Besitz zu nehmen. Doch diese Planung kann schnell zum Verhängnis werden, wenn ein bedrängter Mitspieler durch eine einfache Wanderung eines einzelnen, einsamen Schülers hinein in das große Dorf die notwendige Brückenverbindung in Schutt und Asche zerfallen lässt. Oft genügt schon die Androhung einer solchen Kleinstwanderung, um die Rekrutierung der „Schülerarmee“ sorgevoll vorzeitig abzubrechen. Es gilt also zum einen, möglichst effektiv Schüler zu rekrutieren und Meisterfelder zu übernehmen, zum anderen auch Dörfer geschickt zu schützen oder gar zu isolieren. Fast zwangsläufig ist, dass der eine Spielzug, den man pro Runde machen darf, immer viel zu wenig ist, um alle Pläne auszuführen oder zu durchkreuzen. Die Rechenspiele, in diesem Dilemma den für sich selbst dabei optimalen Zug herauszufinden, gehen bei den Brücken von Shangrila im allgemeinen aber recht zügig von der Hand. Lediglich gegen Spielende, wenn bei knappstem Spielstand die letzten, spielentscheidenden Züge ausgeführt werden sollen, können Rechner den Spielfluss arg ins Stocken bringen – eine Variante (s. unten) kann Abhilfe verschaffen.

Erinnert das Spiel auf den ersten Blick durch seinen Mechanismus zunächst etwas an „Clans“ vom selben Autor, wird bei den ersten Partien schnell klar, dass hinter dem neuen Kosmos-Spiel mehr Spieltiefe, mehr Abwechslung und mehr Raffinesse steckt als im bereits keinesfalls schlechten „Vorgänger“. Das Dilemma, stets zwischen mehreren verlockenden Zugmöglichkeiten entscheiden zu müssen, und die diebische Freude, Planungen der Mitspieler zu durchkreuzen, halten das Spiel stets bis zum Ende des Wettstreits spannend. Wer ein leicht zu erlernendes, taktisches Spiel mit Tiefgang und ohne Glücksfaktor sucht, findet hier tatsächlich das versteckte (Spiele-)Paradies, von dem James Hilton in hellseherischer Weise schon 1933 geträumt haben mag. :-)

Rezension Steffen Stroh

Anmerkung: Zur besseren Lesbarkeit der Texte verwenden wir häufig das generische Maskulinum, welches sich zugleich auf weibliche, männliche und andere Geschlechteridentitäten bezieht.

Regelvarianten

Um Rechenspiele gegen Spielende zu vermeiden, und einen kleinen Glücksfaktor ins Spiel zu bringen, kann Spielaufbau und Abrechnung folgenderweise modifiziert werden: Während des Spiels werden die Symbolplättchen von allen Spielern durch Sichtschirme verdeckt gehalten (basteln oder aus anderen Spielen wie „Samurai“ oder „Medina“ entleihen). Sobald ein Dorf isoliert und mit einem Stein der Weisen belegt wurde, werden alle Meisterplättchen des Dorfes in ein von den Spielern nicht einzusehendes Behältnis geworfen (dazu kann man auch gut das Packungsinlay, verdeckt durch den Spieledeckel oder die Anleitung, verwenden). Die Schülerplättchen kommen in ein separates Behältnis (separate Vertiefung des Inlays). Erst bei Spielende werden die Plättchen wieder hervorgeholt und ausgezählt.